Freeware to Add/Move Unallocated Space to C Drive on Windows 11/10/8/7/Server

How to create unalllocated free space on the same disk

Unallocated space is the partition space which has not been occupied by any drive/data, unallocated space is free space. You can move unallocated space to C drive or any drive to resize partition.

The question: how to produce unallocated space?

Answer: Shrinking large volume on the same disk with Disk Management or free software IM-Magic Partition Resizer. Or you may delete a volume to create unallocated space too.

Part 1 - Create unallocated space with Disk Management Tool by shriking or deleting another volume

A photo that shows you may right click the large volume -> Shrink Volume in Disk Management to create unallocated space.

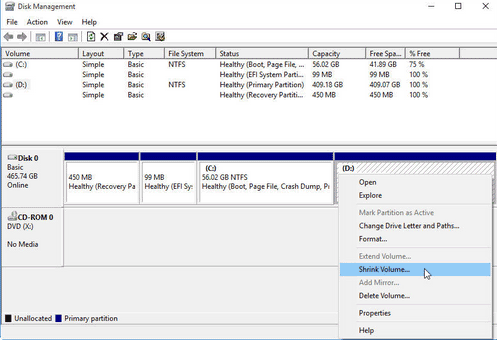Shrinking partition on Windows 7/8/10 for free to create free space

Note: Disk Management or diskpart command is able to shrink/delete volume, however it cannot move unallocated space to c drive if it was produced on the right side of D drive or another drive after the shrinking or deleting. You may use the following free tool Partition Resizer to move unallocated space free to any drive.

Part 2 - Create/move unallocated space with Partition Resizer (free)

Photos show that you may shrink volume without losing data with IM-Magic Parition Resizer.

For Windows 11/10/8/7/Vista ==> Download IM-Magic Partition Resizer Free (Free)

For Windows Server all versions ==> Download IM-Magic Partition Resizer Server (Free Demo)

Step 1 - Download, install and open Partition Resizer, right click your large volume such as the D, go to option "Resize/move Partition"

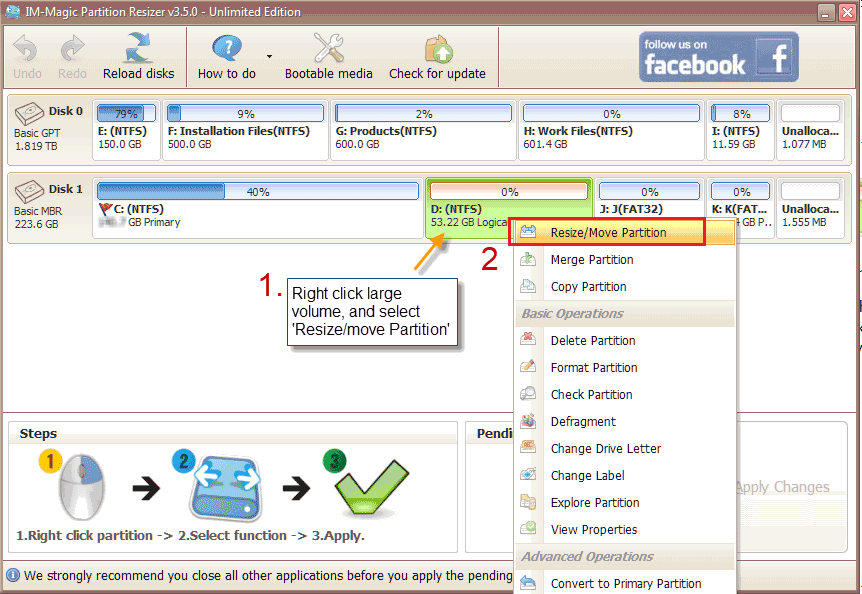Shrink partition on Windows 7/8/10 for free to create free space

Step 2 - Move the border of the D rive rightward, and then the free unallocated space can be produced right after C drive.

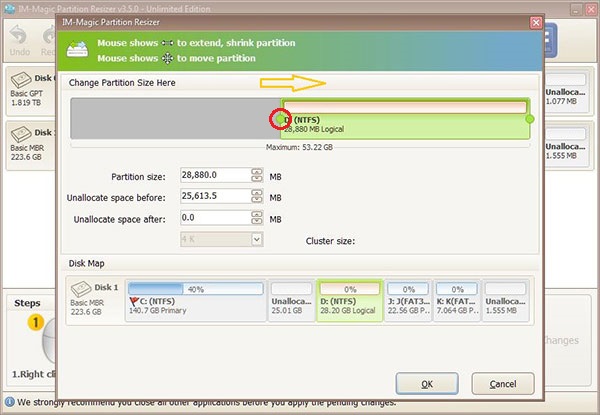Shrink partition on Windows 7/8/10 for free to create free space

Step 3 - Right click c drive, go to RESIZE/MOVE PARTITION option

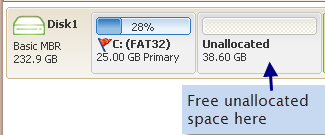Extend c drive with unallocated space in Partition Resizer

Step 4 - Drag the border of the c drive to claim the unallocated space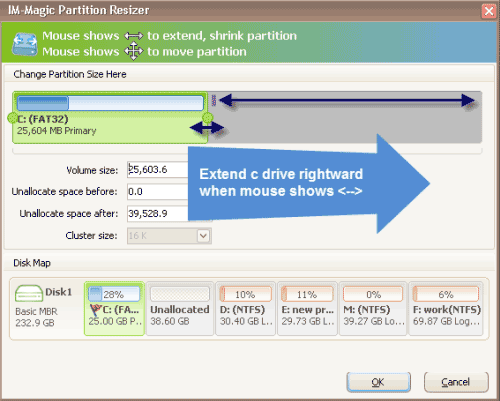

Step 5 - Click the APPLY CHANGES in the software to get the drive expanded.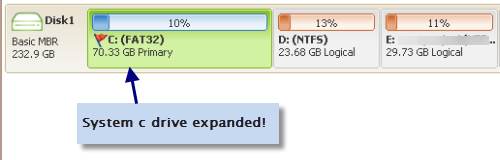

How to Move Unallocated Space to C Drive When It Is NON-Adjacent Space

When there are partitions or volumes between the drive you want to expand and the unallocated space, moving unallocated space without losing data with Partition Resizer that ensures 100% no data loss.

For example, when the disk volume maps like C, D, E, F when there is unallocated space right to E drive, how to move the free space to C?

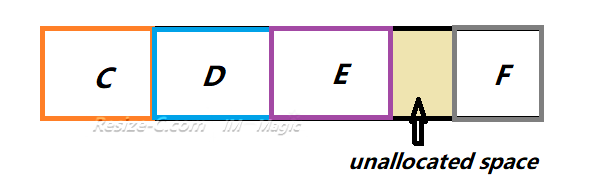
Solution: Move E drive right forward, the free unallocated space will be next to D drive; Move D drive right foward, the unallocated space will be moved to the C drive for extending.

Video - Move Unallocated Space Without Losing Files

Here are the steps.

• Step 1 - Shrink E drive to produce unallocated space by right click E drive in Resizer, and go to 'Resize/move partition', drag the border leftward and then the free unallocated space will be on the right side of E drive
• Step 2 - Right click E drive, and move the whole drive right ward, the unallocated space will be moved to the right side of D drive
• Step 3 - Right click D drive, go to option 'Resize/move Partition', and move the whole D drive right forward, and then the unallocated space will be next to the C drive to be claimed.
• Step 4 - Right click C drive, go to 'Resize/move Partition', move the c drive border right to claim the whole free unallocated space
• Step 5 - Click 'Apply' button to get everything become true

Also read: how to merge non-adjacent (nocotiguous) unallocated space to c drive

How to Move Unallocated Space from Another Disk to C Drive

Condition: RAID

If the unallocated space is on another disk of your computer, it can be moved to C volume or any drive on another disk with the help of RAID (Hardware RAID, no matter what levels of RAID) and Partition Resizer without losing data.

Knowledge: How to build raid arrays

Video - how to build RAID arrays on Windows 10

Extend C Drive with Windows Disk Management

Condition: There must be unallocated space next to c drive (You may delete nearby partition to create some unallocated free space)

The Case: If it's not the c drive's nearby partition you delete, the free unallocated space will be next to some other drive that you cannot move the unallocated space with Disk Management but free tool Partition Resizer can move unallocated space to any drive without losing data.

Step 1 - You can find Disk Management under Computer Manage by the following route.

• Right click THIS PC on desktop -> Manage -> Disk Management

Step 2 - Right click your system drive, you will see a “Extend Volume” option if there is adjacent unallocated space right next to the c drive.

If there is no contiguous unallocated partition, this option 'Extend volume' will be greyed out.

Also read: extend volume greyed out

Step 3 - After you right-click the “Extend Volume” option, you can choose an unallocated partition to add to C drive, after it finished, the system drive can be extended.

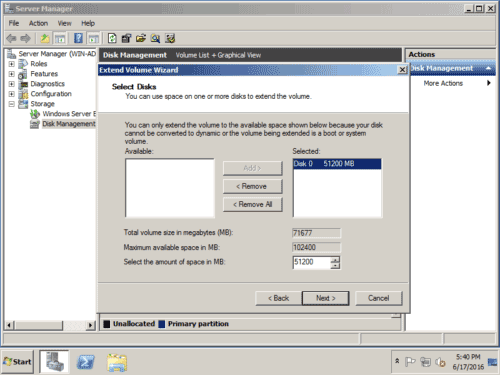Extend C drive on Windows 7/8/10 for free

Move Space to C Drive with Partition Resizer Freeware

If “Extend Volume” function greyed out in your computer, you can try another way to move space to C drive for free. There is a freeware for partition management - IM-Magic Partition Resizer. It is a 100% free software to manage disk partition effectively. (It includes many functions like shrink, extend, merge, split, copy, convert basic to dynamic, convert mbr to gpt etc)

Add Unallocated Space to System Drive for Free

• Scenario #1 - If there is unallocated space next to c drive, you may right click c drive, go to RESIZE/MOVE PARTITION, and extend c drive by dragging the border when the mouse shows double arrow sign
• Scenario #2 - If the unallocated space is not next to the c drive, you may right click the partition that stands in between and go to RESIZE/MOVE PARTITION option to move the whole partition right forward, and then the unallocated space will be close to the drive you want to extend
• Scenario #3 - If there is no unallocated space on the disk, you can shrink some large drive on the same disk to produce unallocated space for redistribution

Tutorial: how to extend c drive with unallocated space next to c drive with free tool Partition Resizer

Step 1: Run -IM-Magic Partition Resizer free on your computer, choose the system drive.

Step 2: Right click “Resize/move partition”. Then you can extend C drive by dragging the mouse.

If there is no unallocated space adjacent to your system drive, you can move some space from other partition or merge partition with C drive.

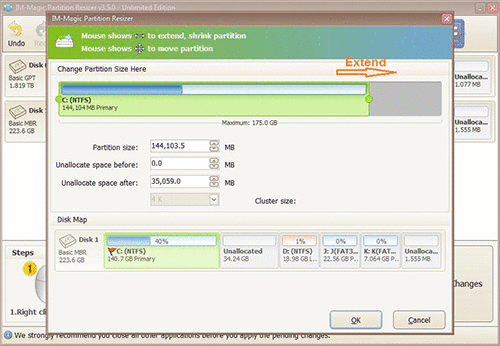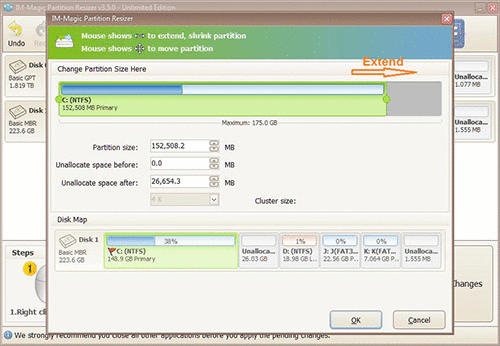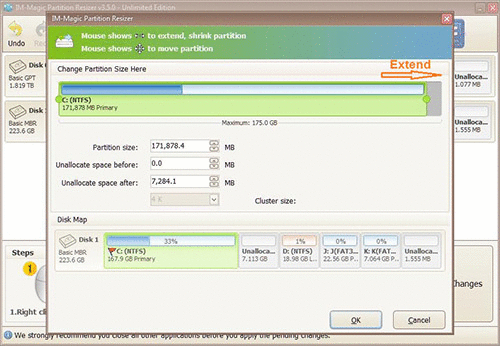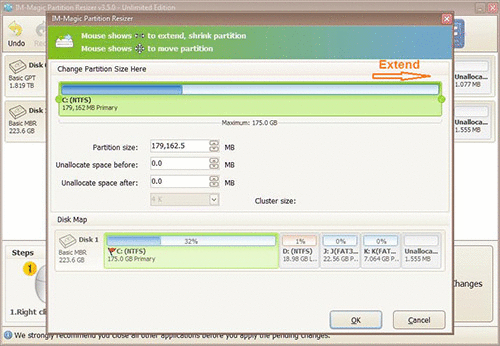Add unallocated space to C drive

Step 3: Apply the changes, and restart your computer.

Then you can have your C drive extended.

If your system is Windows Server system, you can download IM-Magic Partition Resizer Server edition.

Download Resizer Server