Partition Magic for Server 2003, Windows SBS 2003 Download
Summary
This page will tell you the solution to resize disk partition on Windows Server 2003, sbs 2003 with help of partition Magic Server named IM-Magic Partition Resizer Server.
Resize Disk Partition with Partition Magic Server
The problem: PowerQuest Partition Magic does not support Windows Server.
Solution: When you want to resize disk partition on Windows Server, you can download IM-Magic Partition Resizer Server, which is able to be compatible with all Windows Server OS including the Server 2003 operating system to extend or shrink disk partition effectively. By relying on this server magic software, IM-Magic Partition Resizer Server, you can resize both NTFS and FAT32 partition without reinstalling system, reformatting hard disk or repartitioning the disk.
If you right-click a partition in Partition Resizer, you will see the following options. Details may vary depending on the volume properties.
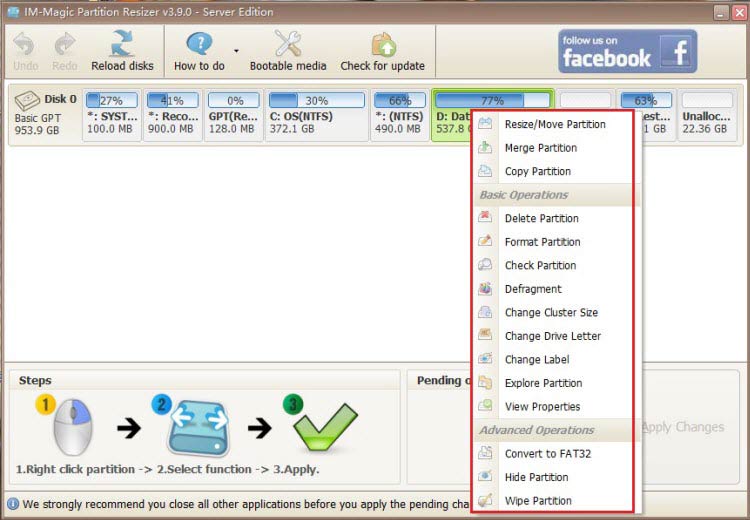
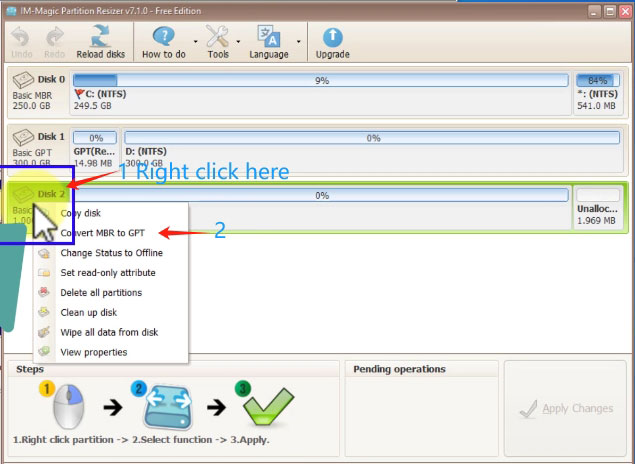
If you right-click a disk in Partition Resizer, different options will appear based on the disk properties.
Step-by-step Guide to Extend C Partition with Resizer
For Windows 11/10/8/7 => Download Partition Resizer Free [100% Free]
For Windows Server 2025-2003 => Download Partition Resizer Server [Free Demo]
How to redistribute disk space in Windows Server?
Step 1:
Download, install and launch IM-Magic Partition Resizer Server. Right click a partition that
has lots of free disk space and choose "Resize/Move".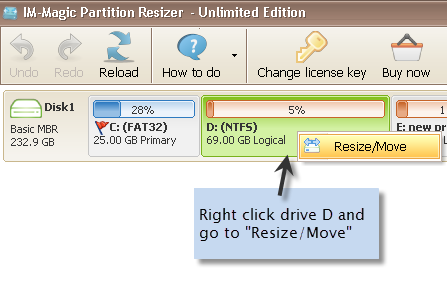
Step 2:
When seeing mouse shows double arrows, you can shrink the selected partition to squeeze some
free space from it. The free space will be shown as unallocated volume.
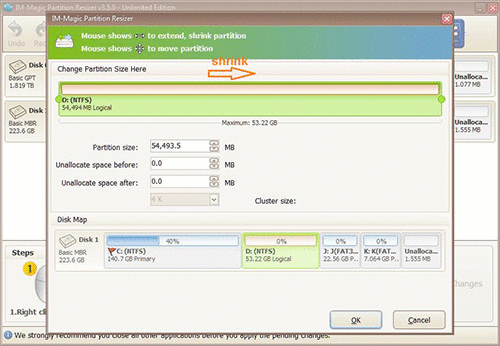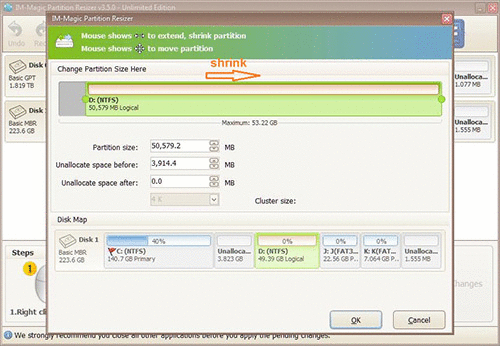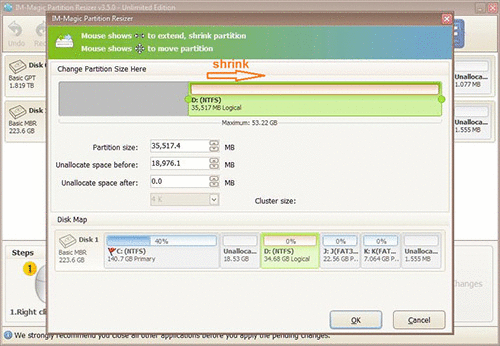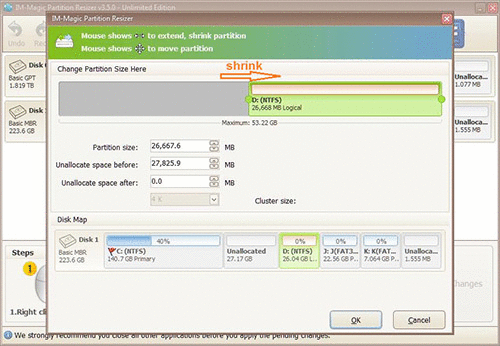
Steps to resize your disk partition
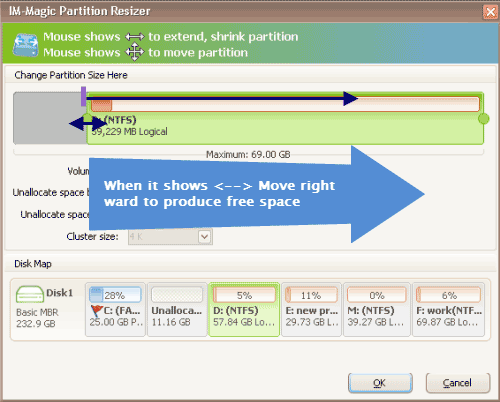
Shrink other large partition to produce free space for C drive
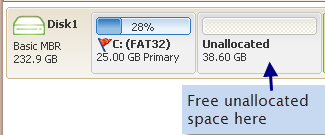
Step 3:
Move the unallocated volume close to C partition. Right click C partition and choose
"Resize/Move".
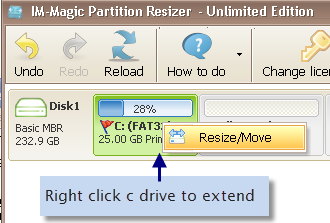
Right click c drive to get started with extending c
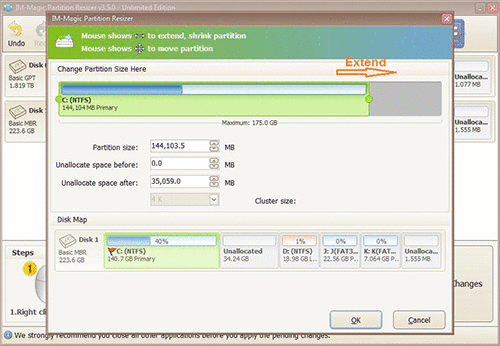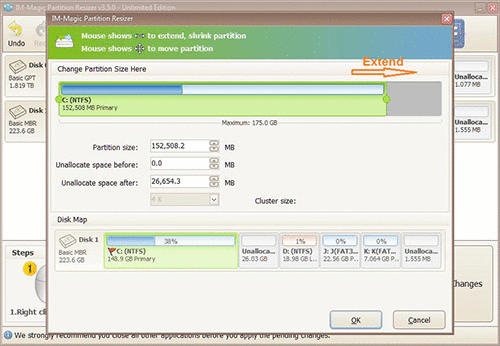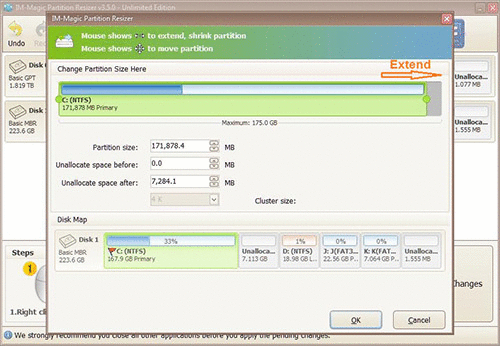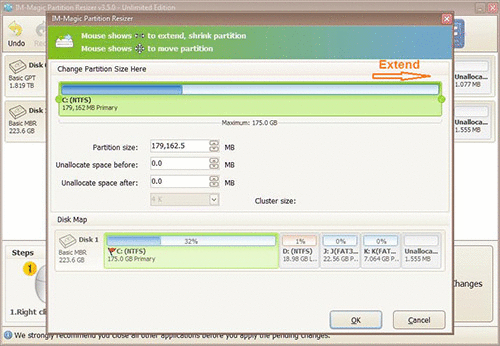
Steps to resize your disk partition
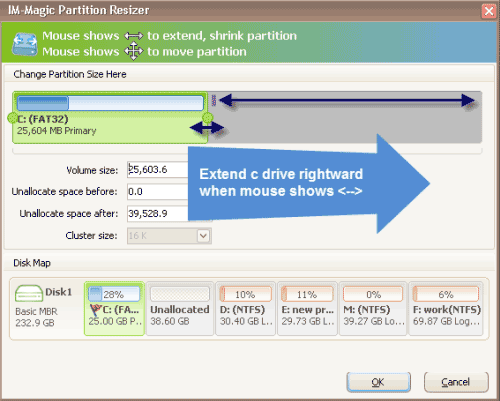
Step 4:
When mouse shows double arrows, you can move the arrow to increase the size of C partition.
Finally, you need to click "Apply" button to get C partition extended.
Disk Partition Runs Low Disk Space on Server 2003
Windows Server 2003 is the most widely used Server operating system among computer users. When installing the Server 2003 system, disk partitions have been allocated. However, the free space of each disk partition will become less and less as time goes by. Finally, you may find that the scheduled size of some partition will fail to meet your needs to store more data. This kind of problem occurs on system partition more frequently because not only operating system and system related programs are installed on this partition, but also every time you browse a site or open a file, the temporary files, cookies, etc are also stored on this partition.
Extend Disk Partition on Windows Server 2003
It cannot free much space by deleting old or unnecessary files, so the space will be eaten up soon. The best way to solve the problem when windows 2003 shows low disk space warning on system partition or data partition is to extend the partition. On Windows Server 2003, you have two solutions to extend a partition. We will introduce the two solutions, so you can select a proper one to increase the size of disk partition without formatting the disk.
The First Solution, Extend a NTFS Partition by Diskpart Command
Diskpart command is a Windows built-in disk management tool, with which you are able to
create a partition, delete a partition, extend a partition, etc. Therefore, you can run Diskpart command to extend disk
partition when it is running on low disk space. Diskpart command works as partition
magic tool at most time, but it still has limitations.
Firstly, Diskpart command only enables you to extend NTFS partition. If you want to extend
an FAT32 partition, Diskpart command may fail.
In addition, you must ensure that there is free space right behind the partition you want to
extend. If there is no free space, or if the free space is not right behind the partition,
Diskpart command cannot work either
The Second Solution, Extend Partition with Partition Magic Server
When you are unable to extend partition with help of Diskpart command, you can try the second
solution. You may run IM-Magic Partition Resizer Server, which also works as partition magic
without any limitation. You are allowed to extend both NTFS and FAT32 partition with this
partition magic software. Free space is also required in order to extend a partition with
IM-Magic Partition Resizer Server. If there is no free space, you can this partition magic software to
shrink a partition to squeeze some free space. If the free space is not close to the
partition you want to extend, you can also move the free space close to the partition you
need to extend with help of IM-Magic Partition Resizer Server.
By using this partition magic software, you don’t need to move or backup any data because it
doesn’t have any influence on the disk partition during partition resizing. This partition
magic software won’t hurt the system either, so you can completely rely on it.
